逆波兰表示 基础知识介绍完了，进入正题：如何编写一个程序来进行四则运算呢？ 我们看到 12 +（3 + 4）* 5 / 7 可以很快就算出来答案是 17，因为我们知道要先计算括号里面的加法，然后先乘除，后加减，最后得到计算结果。可是对计算机程序来说，输入是一个字符串，需要区分数字、运算符、括号，然后需要按照前面的运算顺序执行，才能得到结果。 为了更好地编程实现四则元算，我们要引入一个新的算数表示法——逆波兰表示，之所以叫这个名，是因为它的发明者是一位波兰的数学家。在逆波兰表示中，操作符（ +，-，，/ ) 是位于操作数后面的，而不是位于中间。举个简单的例子，3 + 4 的逆波兰表示就是 3 4 +。12 +（3 + 4） 5 / 7 的逆波兰表示是 12 3 4 + 5 7 / * +。 逆波兰表示转化的算法及代码 如何把我们熟悉的四则运算表达式转化为逆波兰表示呢？ 还是要利用栈的后进先出特性。下面简要描述将常规四则元算表达式转化为逆波兰表示的步骤： 创建一个空栈。 从左至右遍历常规四则元算表达式的字符，对每一个字符：

1. 若字符是数字，则将其添加到输出的表达式的尾端；
2. 若字符是左括号 "("，则将其入栈；
3. 若字符是 "+" 或者 "-"，则把栈中元素依次出栈，添加到输出表达式的末尾，直到栈顶元素是左括号 "(" ， 或者栈变为空栈，再把字符入栈；
4. 若字符是 "*" 或者 "/"，则将其入栈；
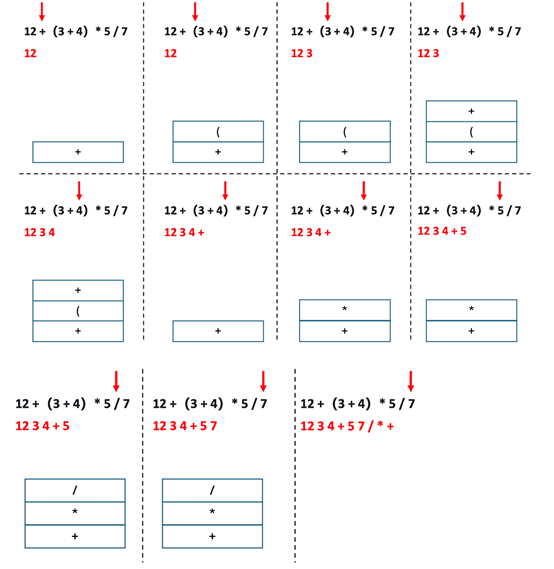
5. 若字符是有括号 ")"，则把栈中元素依次出栈，添加到输出表达式末尾，直到栈顶元素是是左括号 "("，然后将左括号出栈。 遍历玩所有字符以后，如果栈非空，则将栈中元素依次出栈，添加到输出表达式末尾。 下图显示了将 12 +（3 + 4）* 5 / 7 转化为逆波兰表示过程中，栈中元素以及输出表达式的变化。

逆波兰表达式求值 有了逆波兰表达式，求值就变的很方便了。还是需要利用栈后进先出的特性。下面是对逆波兰表示的求值步骤： 创建一个空栈。 从左至右遍历逆波兰表达式：

1. 若当前元素为数值，则入栈；
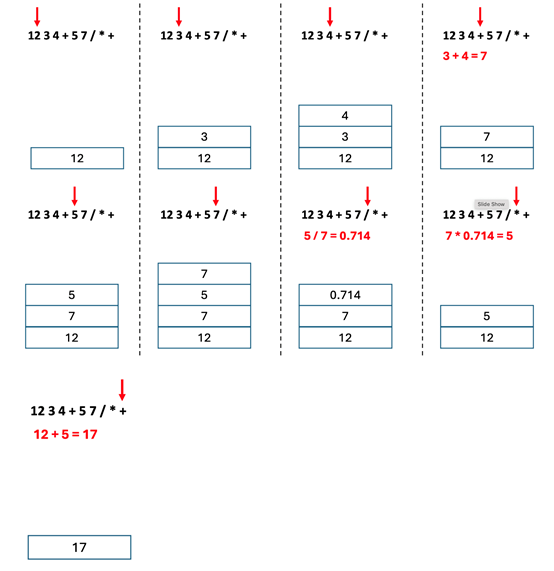
2. 若当前元素为运算符，则将栈顶两个元素出栈，以它们作为操作数，当前元素为操作符，进行运算，将运算结果入栈。 当遍历完成时，栈顶元素出栈，即为最终运算结果。 注意，在逆波兰表示中，连续的数字需要用一定的标记符号来隔开，在这里，我用的是空格符号。在上面的算法中，没有提到这一点，但是在写代码的时候，需要注意。 下面是遍历逆波兰表达式 12 3 4 + 5 7 / * + 求值的过程。

#include<iostream>
#include<cstdio>
#include<string>
#include<stack>
using namespace std;

stack<char> s;      // 用于中缀转后缀的运算符栈
stack<int> ss;      // 用于计算后缀表达式的数字栈

int main() {
    int len1, len2, len, i, j;
    string str1, str2;  // str1为中缀表达式，str2为后缀表达式
    
    while(1) {
        // 中缀表达式转换为后缀表达式
        getline(cin, str1);
        len1 = str1.length();
        str2.clear();
        
        // 第一步：将中缀表达式转为后缀表达式
        for (i = 0; i < len1; i++) {
            // 情况1：如果是数字，直接加入后缀表达式
            if (str1[i] >= '0' && str1[i] <= '9') {
                str2.push_back(str1[i]);
            }
            // 情况2：如果栈为空或者是左括号，直接入栈
            else if (s.size() == 0 || str1[i] == '(') {
                s.push(str1[i]);
            }
            // 情况3：遇到右括号
            else if (str1[i] == ')') {
                // 把栈中的运算符弹出，直到遇到左括号
                while (!s.empty()) {
                    char tmp = s.top();
                    s.pop();
                    if (tmp == '(') break;  // 遇到左括号就停止
                    else str2.push_back(tmp);  // 其他运算符加入后缀表达式
                }
            }
            // 情况4：遇到其他运算符（+ - * /）
            else {
                char tmp1 = s.top();  // 查看栈顶运算符
                
                // 如果栈顶是*或/，且当前也是*或/
                if (tmp1 == '*' || tmp1 == '/') {
                    if (str1[i] == '*' || str1[i] == '/') {
                        s.push(str1[i]);  // 优先级相同，直接入栈
                    } else {
                        // 当前运算符优先级低，先把栈中所有运算符弹出
                        while (!s.empty()) {
                            char tmp = s.top();
                            s.pop();
                            str2.push_back(tmp);
                        }
                        s.push(str1[i]);  // 再入栈当前运算符
                    }
                } else {
                    s.push(str1[i]);  // 栈顶优先级低，直接入栈
                }
            }
        }
        
        // 把栈中剩余的运算符全部弹出
        while (!s.empty()) {
            char tmp = s.top();
            s.pop();
            str2.push_back(tmp);
        }
        
        cout << "后缀表达式: " << str2 << endl;
        
        // 第二步：由后缀表达式计算结果
        int temp1, temp2, temp3;
        len2 = str2.length();
        
        for (i = 0; i < len2; i++) {
            // 如果是数字，转换为整数后入栈
            if (str2[i] >= '0' && str2[i] <= '9') {
                int t = str2[i] - '0';  // 字符转数字
                ss.push(t);
            }
            // 如果是运算符
            else {
                // 从栈中弹出两个数字
                temp1 = ss.top(); ss.pop();
                temp2 = ss.top(); ss.pop();
                
                // 根据运算符进行相应的计算
                if (str2[i] == '+') {
                    temp3 = temp2 + temp1;  // 加法
                } else if (str2[i] == '-') {  // 修正：应该是'-'而不是'_'
                    temp3 = temp2 - temp1;   // 减法
                } else if (str2[i] == '*') {
                    temp3 = temp2 * temp1;   // 乘法
                } else if (str2[i] == '/') {
                    temp3 = temp2 / temp1;   // 除法
                }
                
                ss.push(temp3);  // 计算结果入栈
            }
        }
        
        cout << "计算结果: " << ss.top() << endl;
        ss.pop();  // 清空栈顶
        
        // 可以选择是否继续计算，这里会无限循环
        // 可以添加退出条件，比如输入"exit"时退出
    }
    
    return 0;
}